2019, Oct 07
Pulsar Stars Detection
Predicting a Pulsar Star with Deep Learning¶
1. Motivation¶
Pulsar stars are a very rare type of Neutron star that produce radio emission detectable on Earth and they are of considerable scientific interest as probes of space-time and states of matter. Their emission spreads across the sky and produces a detectable pattern of broadband radio emission. However in practice almost all detections are caused by radio frequency interference and noise, making legitimate signals hard to find.
Having said that, the main purpose of this problem is to build a simple classifier using deep learning tools in order to predict wether a detected signal comes from a pulsar star or from other sources such as noises, interferences, etc.
All information and data related to this problem can be found here: https://www.kaggle.com/pavanraj159/predicting-a-pulsar-star
2. Data Information¶
Each signal is described by eight continuous variables, and a single class variable. The first four are simple statistics obtained from the integrated pulse profile and the remaining four variables are similarly obtained from the DM-SNR curve. These variables are:
Mean of the integrated profile.
Standard deviation of the integrated profile.
Excess kurtosis of the integrated profile.
Skewness of the integrated profile.
Mean of the DM-SNR curve.
Standard deviation of the DM-SNR curve.
Excess kurtosis of the DM-SNR curve.
Skewness of the DM-SNR curve.
Class
The data set shared here contains 17898 total samples.
3. Dependences¶
Here we can find the libraries we will use in order to develop a solution for this problem:
numpy|pandas: Will help us treat and explore the data, and execute vector and matrix operations.
matplotlib|seaborn: Will help us plot the information so we can visualize it in different ways and have a better
understanding of it.
keras: Will provide us all the necessary deep learning tools to develop a solution for the problem.
sklearn: We are using this library since it gives us access to some tools to divide our dataset into training and test and some metrics we can use to evaluate our models.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import keras
from prettytable import PrettyTable
from keras.models import Sequential
from keras.utils.vis_utils import plot_model
from sklearn.metrics import confusion_matrix, accuracy_score, recall_score, f1_score
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from keras.layers import Dense, Dropout
4. Data Exploration¶
Since this is a deep learning solution we do not want to make any feature selection or special treatment to our data. However let's take a quick look at our data and understand it first!
#read the csv that contains our data and print the first 5 rows of it
df = pd.read_csv("pulsar_stars.csv")
df.head()
First of all we observe the name of these columns is quite long and full of spaces, let's rename them:
#Changing the name of some columns
df.columns = ['mean_profile', 'std_profile', 'kurtosis_profile', 'skewness_profile', 'mean_dmsnr',
'std_dmsnr', 'kurtosis_dmsnr', 'skewness_dmsnr', 'target']
Now let's look for null values and object datatypes we might want to transform into numerical values:
#Looking for null values
df.isna().sum()
#Looking for object datatypes
df.info()
After having checked there are no null values and all columns contain numerical values, let's take a look at some information about our data:
#Show statistical information of our data
df.describe()
Just by looking at this table we can extract some important information of our data, for example if we take a look at the target column we can see the max value is 1 (pulse star) and the minimum value is 0 (not a star) while the mean of this column tends to 0, which lets us know there are more "false pulse stars" than actual stars. Additionally we clearly see this data needs some scaling since the difference between values is noticeable.
5. Data Visualization¶
At this point we are going to plot some things that might be of our interest from this dataset. First of all knowing our target variable let's see the difference between values, or better said, the proportion between them:
#counting pulsars and not pulsars
pulsar = df[df['target'] ==1]
pulsar_count = pulsar["target"].value_counts()[1]
not_pulsar = df[df['target'] == 0]
not_pulsar_count = not_pulsar["target"].value_counts()[0]
#pie plotting the stats between pulsars and not pulsars
plt.figure(figsize=(5,5))
plt.pie(df["target"].value_counts().values,labels=["not pulsar stars","pulsar stars"], autopct="%1.0f%%")
plt.title("Proportion of target variable in dataset")
plt.show()
print("There are " + str(pulsar_count) + " signals that belong to pulsar stars "
+ "and " + str(not_pulsar_count) + " signals that aren't from pulsars.")
From the graph above we see that approximately the 10% of our samples are real Pulsar Stars while the other 90% detected signals belong to something else such as noise. Now let's have a look at how features correlate with each other.
#plot correlation matrix
plt.figure(figsize=(6,6))
sns.heatmap(df.iloc[:,0:9].corr(), annot=True, fmt='.0%')
Something curious we can see from this correlation matrix is that four of the eight features we have in our dataset correlate positively with our target variable whilst the other four correlate negatively; this is really going to help when training our model since the separation between classes becomes clear. Having said that let's go deeper into investigating these features!
#violinlpot of all features
features = df.iloc[:,0:8]
plt.figure(figsize=(15,20))
j = 0
for i in features:
plt.subplot(4,3,j+1)
sns.violinplot(x=df["target"],y=df[i],palette=["red","lime"])
plt.title(i)
plt.axhline(df[i].mean(),linestyle = "dashed", label ="Mean value = " + str(round(df[i].mean(), 2)))
plt.legend(loc="best")
j = j + 1
Thanks to these violin plots we are able to extract information about the distribution of values for each of the features our database contain. Furthermore we can view these distributions for the different values our target variable has, plus having this dashed line being the mean value of the feature might help us understand this data better. That said, let's comment some of the features for which we see the separation between classes becomes more clear:
mean_profile. From the correlation matrix we observed the higher the values the less change of the signal coming from a pulsar star, in our violinplot we clearly see it. Additionally, by looking at the mean we could say that if a mean_profile value is above the mean value, that signal might probably to come from another source than a star.
kurtosis_profile. Like mean profile, this feature is also pretty interesting. We clearly observe how the majority of samples whose kurtosis_profile value is above the mean value belong to the group of pulsar stars while, with some outliers that break the rules, lower values than the mean come from other signals. In addition, the distribution of values from the "non pulsar" group is pretty similar, meaning the range of kurtosis_profile values for those signals is quite narrow and the opposite happens to the pulsar group, values tend to be in a range between 0.48-8.
skewness_profile. From skewness_profile we can extract a quite interesting information. It actually seems weird the mean value is just 1.77 when we have values higher than 60 in our dataset. The reason for that is that in our dataset we have approximately 10 times more "non-pulsar" than actual pulsar stars and the majority of skewness values for the non pulsar are pretty close to 0; since the pulsar group is proportionally smaller the mean value is penalized. However that gives us a very important information, the majority of samples whoso skewness_profile value is higher than the mean will probably belong to the pulsar group and, we could say almost 100% samples whose value is higher than 23~ are stars!
mean_dmsnr/skewness_dmsnr. These features are pretty similar in terms of data distribution with the difference being that in mean_dmsn the vast majority of negative star values lay under the mean and in skewness_dmsnr it's exactly the oppositve, pulsar stars are located under the mean value. That said, these distributions look very similar to the one we commented before (skewness_profile) but with one exception: here we can't surely affirm that from "x" value above or below the mean value each sample will belong to a pulsar or not pulsar star, since the range of values for these features is pretty wide.
In order to make sure our hypotesis of data being easily separable for the majority of features is true, we are going to create a pairplot between columns and check if we can visually make that separation.
#pairplot between features
sns.pairplot(df, hue="target", palette=["red","lime"])
Thanks to pairplotting it's clear that our data seems to be split in two huge separated groups that can be easily differentiated by just looking at the graphic above.
6. Preparing and Fitting Our Deep Learning Model¶
Now it's time to prepare our Deep Learning model and, unlike in Machine Learning, we are not going to select any specific features, we are going to set some parameters that we think are going to make the neural network perform and its best and then feed it with all our data. That said, we may still have to split our data into training and set (validation might be OK as well) and scale our data too, if needed.
#Separing our features from target variable
X = df.iloc[:,0:8].values
y = df.iloc[:,8].values
#Scaling our data
sc = StandardScaler()
X = sc.fit_transform(X)
#Splitting data
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size = 0.3)
Now that we have our data scaled and split into training and test, it's time to define our deep learning model. We are going to use a Sequential model since we want to create our model layer by layer. We are going to be creating a simple fully-connected neuronal network with 3 total layers (2 of them as hidden layers and 1 output layer). Between these layers we are going to use Dropout layers in order to reduce overfitting and we're setting the rate as 0.3.
The input dimension is 8 since we're using eight features and output dimension as 1 since we're only receiving one label. The number of neurons per layer has been chosen randomly without being excessively high after having tried with bigger and lower numbers and observing the results barely variate. It's also important to mention that, after having tested other activation functions for hidden layers, we're using relu as activation function since it provided slightly better results and sigmoid for the output layer since this is a binary classification problem. For the output layer we could also use a softmax activation function but, since this is not a multi class classification problem but a binary, there is no real use of using it since it may decrease our accuracy by 2-3%.
#define a sequential Model
model = Sequential()
#First hidden layer
model.add(Dense(16,activation='relu',input_dim=8))
model.add(Dropout(0.25))
#Second hidden Layer
model.add(Dense(8,activation = 'relu'))
model.add(Dropout(0.25))
#Output layer
model.add(Dense(1,activation='sigmoid'))
Having already our model defined there comes the time to compile it. As loss function we're using binary_crossentropy since, as we've already said, this is a binary classification problem. We're aso using adam as optimizer since adapts the learning rate as the training progresses and as far as metrics are concerned we're using accuracy.
#Compiling the model
model.compile(loss='binary_crossentropy',optimizer='adam',metrics=['accuracy'])
#Printing a summary of our model
model.summary()
We can see our model in a table above, but let's show an image of how it really looks like. To do so we have used the Kaggle build-in python editor since it already has all the necessary libraries installed and we only want the picture of it. That said, here's the picture that describes our model:
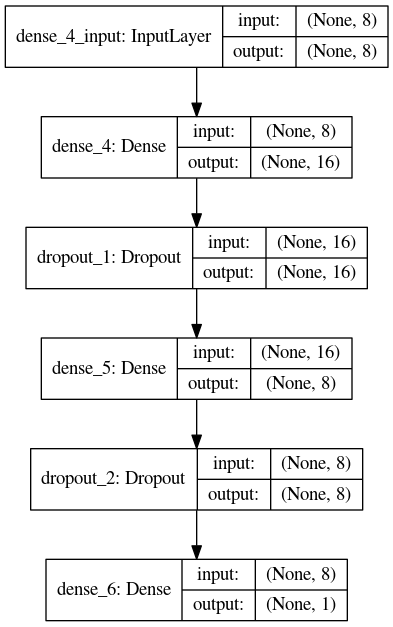
Now it usually comes the time to fit our model. However before doing that it might be interesting to adjust the weight of our different output classes, in other words since our database has way more values that don't belong to pulsar stars, we really want to set a higher importance rate to those samples who really come from stars. That's something called handling imbalanced datasets and might help our model to predict, hopefully, our positive pulsar stars samples better.
#Adjusting class weights
weight = {0 : 1., 1 : 2.}
Having done that, let's fit our model!
#Fitting our model with training data and, at the same time, using test data for validation
history = model.fit(X_train, y_train, epochs=100, batch_size=64, class_weight=weight, validation_data = (X_test,y_test), verbose=2)
As we can see our model works pretty well (note that we only show the last two Epochs)! We get an accuracy score of 98% approximately for both our training and test data
7. Evaluating Our Model¶
In order to do this evaluation we're going to do two things. First of all we're going to plot the model accuracy and loss for each the training and validation data, and afterwards we're going to make a prediction and, through a confussion matrix, see how it goes.
#Visualizing accuracy for both training and test data
plt.plot(history.history['accuracy'])
plt.plot(history.history['val_accuracy'])
plt.title('Model Accuracy')
plt.ylabel('Accuracy')
plt.xlabel('Epoch')
plt.legend(['Train', 'Test'], loc='lower right')
plt.show()
As interesting as it may seem, we can observe how the accuracy of our model keeps practically the same after 10 Epochs, in our case we're using 100 since it might prevent overfitting.
#Visualizing loss for both training and test data
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('Model Loss')
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.legend(['Train', 'Test'], loc='upper right')
plt.show()
With our two graphics already here let's make a prediction and see the confussion matrix:
#Confussion Matrix
label_aux = plt.subplot()
prediction = model.predict(X_test)
cm = confusion_matrix(y_test, np.round(prediction))
cm_nn = pd.DataFrame(cm, index = ['Not a Star','Star'], columns = ['Not a Star','Star'])
sns.heatmap(cm_nn,annot=True,fmt="d", cbar=False)
label_aux.set_title("Confussion Matrix of Our Model")
label_aux.set_xlabel('Predicted Value');label_aux.set_ylabel('True Value');
#Printing some metrics
ptbl = PrettyTable()
ptbl.field_names = ["Accuracy", "Recall", "F1Score"]
ptbl.add_row([accuracy_score(y_test,np.round(prediction)),recall_score(y_test, np.round(prediction)),
f1_score(y_test, np.round(prediction))])
print(ptbl)
8. Conclusions¶
After solving this problem using Deep Learning we have come to the following conclusions:
- Our Deep Learning model predicts very well wether a signal comes from a pulsar star or another external source.
- Thanks to data being clearly separable in two groups (pulsar and not pulsar), our model has worked very well.
- Had we happened to have used a Machine Learning algorithm instead of Deep Learning techniques, feature engineering would have been clear since there is a strong correlation on this dataset.
- The number of Epochs (iterations) in our Neural Network could have been reduced since results were pretty much the same after the first 40 iterations but having a higher number of Epochs might prevent overfitting.
- There are some features that are really well separated as we have explained when plotting the violins. It could be easy to predict the target class just by looking at a sample if some values where below or above the mean value.
- This dataset is quite imbalance since there are only 10% of samples that belong to pulsar class; adjusting weights before feeding data to our neural network might help us detecting True Positives, which is what we're interested in.
In case someone wants to know how to solve this particular problem using different Machine Learning algorithms, this following link will take you to a very interesting Kernel where the author solves it using different techniques explaining the algorithms he uses as well as what he is doing each step.
